
ウェブページの重要性は本質的に主観的な問題であり、読者の興味、知識、態度によって異なります。しかし、ウェブページの相対的な重要性について客観的に語れることはまだ多くあります。本論文では、ウェブページを客観的かつ機械的に評価し、人々の関心と注目度を効果的に測定する手法であるPageRankについて説明します。
PageRankを理想的なランダムなウェブサーファーと比較します。多数のページのPageRankを効率的に計算する方法を示します。そして、PageRankを検索とユーザーナビゲーションに適用する方法を示します。
ワールド・ワイド・ウェブは、情報検索において多くの新たな課題を生み出しています。ウェブは非常に大規模で、多種多様な情報で構成されています。現在、倍増寿命が1年未満のウェブページは1億5000万ページ以上あると推定されています。さらに重要なのは、ウェブページが極めて多様であり、「ジョーは今日何を食べているのか?」という情報から情報検索に関するジャーナルまで多岐にわたることです。こうした大きな課題に加えて、ウェブ上の検索エンジンは、経験の浅いユーザーや、検索エンジンのランキング機能を操作するように設計されたページにも対処しなければなりません。
しかし、「フラット」な文書集合とは異なり、ワールド・ワイド・ウェブはハイパーテキストであり、ウェブページのテキストに加えて、リンク構造やリンクテキストといった多くの補助情報を提供します。本稿では、ウェブのリンク構造を利用して、すべてのウェブページのグローバルな「重要度」ランキングを作成します。PageRankと呼ばれるこのランキングは、検索エンジンとユーザーがワールド・ワイド・ウェブの広大な異質性を迅速に理解するのに役立ちます。
学術引用分析に関する文献はすでに多数存在しますが、ウェブページと学術出版物の間には多くの重要な違いがあります。綿密に査読される学術論文とは異なり、ウェブページは品質管理や出版コストを伴わずに増殖します。単純なプログラムで膨大な数のページを簡単に作成でき、引用数を人為的に水増しすることができます。ウェブ環境には利益追求を目的とした競合関係が存在するため、注目を集める戦略は検索エンジンのアルゴリズムに応じて進化します。そのため、ウェブページの再現可能な機能を数える評価戦略は、操作されやすい傾向があります。さらに、学術論文は明確に定義された作業単位であり、質と引用数、そして知識体系の拡張という目的においてもほぼ同等です。ウェブページは、質、利用状況、引用、長さにおいて、学術論文よりもはるかに大きなばらつきがあります。IBMコンピュータに関する難解な質問を投稿したランダムなアーカイブメッセージは、IBMのホームページとは大きく異なります。携帯電話の使用が運転者の注意力に与える影響に関する研究論文は、特定の携帯電話会社の広告とは大きく異なります。ユーザーが体験する平均的なウェブページの品質は、平均的なウェブページの品質よりも高くなります。これは、ウェブページの作成と公開が簡単であるため、ユーザーが読む可能性の低い低品質のウェブページが大量に発生するためです。
ウェブページを差別化する軸は数多く存在します。本稿では、主にその一つ、ウェブページの全体的な相対的重要度の近似値について扱います。
ウェブページの相対的な重要度を測定するために、ウェブグラフに基づいて各ウェブページのランキングを計算する手法であるPageRankを提案します。PageRankは、検索、ブラウジング、トラフィック推定などに応用されています。
第2節では、PageRankの数学的説明と、その直感的な根拠を示します。第3節では、最大5億1800万のハイパーリンクに対してPageRankを効率的に計算する方法を示します。検索におけるPageRankの有用性を検証するために、GoogleというWeb検索エンジンを構築しました(第5節)。また、第7.3節では、PageRankをブラウジング支援としてどのように活用できるかを示します。
学術論文の引用分析に関する研究は数多く行われてきました[Gar95]。Goffman[Gof71]は、科学コミュニティにおける情報の流れがいかにして伝染病のようなプロセスであるかという興味深い理論を発表しました。
近年、Webのような大規模ハイパーテキストシステムのリンク構造を活用する方法について、かなりの研究が行われています。Pitkowは最近、「ワールド・ワイド・ウェブの生態系の特徴づけ」[Pit97, PPR96]という博士論文を執筆し、様々なリンクベースの分析を取り上げています。Weissは、リンク構造を考慮したクラスタリング手法について論じています[WVS* 96]。Spertusは[Spe97]、様々なアプリケーションのためにリンク構造から得られる情報について論じています。優れた視覚化にはハイパーテキストに構造を追加する必要があり、これについては[MFH95, MF95]で議論されています。最近、Kleinbergは[Kle98]、Webの共引用行列の固有ベクトル計算に基づいて、Webをハブとオーソリティとして捉える興味深いモデルを開発しました。
最後に、図書館コミュニティからは、ネット上での「品質」が何を意味するのかという点に関心が寄せられています[Til]。
標準的な引用分析手法をウェブのハイパーテキスト引用構造に適用しようとするのは当然のことです。すべてのリンクを学術的な引用と考えるだけで十分です。つまり、http://www.yahoo.com/ のような主要なページには、数万ものバックリンク(または引用)がリンクしていることになります。
Yahoo!のホームページにこれほど多くのバックリンクがあるという事実は、一般的に、それが非常に重要であることを示しています。実際、多くのウェブ検索エンジンは、バックリンクの数を、データベースをより高品質またはより重要なページに偏らせるための手段として利用しています。しかし、単純なバックリンクの数には、ウェブ上でいくつかの問題があります。これらの問題のいくつかは、通常の学術引用データベースには見られない、ウェブの特性に関係しています。
推定値は様々ですが、現在クロール可能なWebのグラフには、およそ1億5000万のノード(ページ)と17億のエッジ(リンク)があります。すべてのページには、一定数のフォワードリンク(アウトエッジ)とバックリンク(インエッジ)があります(図1参照)。特定のページのバックリンクをすべて見つけたかどうかはわかりませんが、ページをダウンロードしていれば、その時点でのフォワードリンクはすべてわかります。

ウェブページは、そのバックリンクの数によって大きく異なります。例えば、Netscapeのホームページは、現在のデータベースでは62,804ものバックリンクを持っていますが、ほとんどのページはバックリンクが数個しかありません。一般的に、リンク数の多いページは、リンク数の少ないページよりも「重要」です。単純な引用回数のカウントは、ノーベル賞の将来の受賞者を予想するために使われてきました[San95]。PageRankは、より洗練された引用回数のカウント方法を提供します。
PageRankが興味深いのは、単純な引用数カウントが、私たちの常識的な重要性の概念と一致しない場合が多いからです。例えば、あるウェブページにYahoo!のホームページからのリンクがある場合、それはたった1つのリンクかもしれませんが、非常に重要なリンクです。このページは、より多くのリンクがあるものの、あまり知られていない場所からのリンクを持つ多くのページよりも上位にランク付けされるべきです。PageRankは、リンク構造のみから「重要性」をどの程度正確に推定できるかを測る試みです。
上記の議論に基づき、PageRankについて直感的に次のように説明します。ページのバックリンクのランクの合計が高い場合、そのページのランクは高くなります。これは、ページに多数のバックリンクがある場合と、ページに少数の高ランクのバックリンクがある場合の両方に当てはまります。
\(u\) をウェブページとします。\(F_u\) を \(u\) が指し示すページの集合、\(B_u\) を u を指し示すページの集合とします。\(N_u = |F_u|\) を u からのリンク数とし、c を正規化に用いる係数とします(これにより、すべてのウェブページの合計ランクは一定になります)。
まず、PageRank を少し簡略化したシンプルなランキング \(R\) を定義します。 \[ R(u)=c\sum_{v\in B_u} \frac{R(v)}{N_v} \]
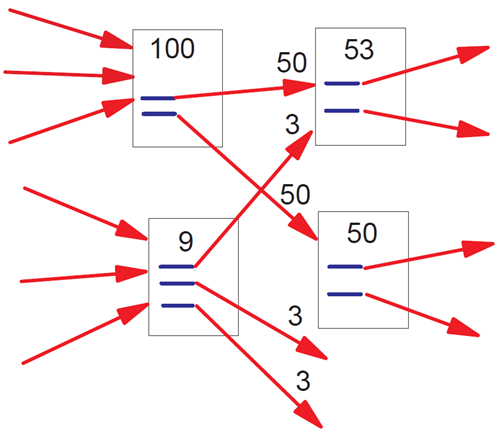
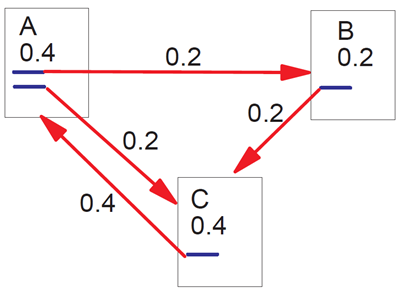
これは、前の節での直感を形式化したものです。ページのランクは、その前方リンクに均等に分配され、それらが指すページのランクに寄与することに注意してください。\(c < 1\) であることに注意してください。これは、前方リンクのないページが多数存在し、それらの重みがシステムから失われるためです(2.7節を参照)。この式は再帰的ですが、任意のランクの集合から開始し、収束するまで計算を繰り返すことで計算できます。図2は、あるページペアから別のページペアへのランクの伝播を示しています。図3は、ページセットに対する一貫した定常解を示しています。
言い換えると、\(A\) を、行と列がウェブページに対応する正方行列とします。\(u\) から \(v\) への辺がある場合は \(A_{u,v} = 1/N_u\)、ない場合は \(A_{u,v}= 0\) とします。\(R\) をウェブページ上のベクトルとして扱うと、\(R = cAR\) となります。つまり、\(R\) は \(A\) の固有ベクトルであり、固有値は \(c\) です。実際、私たちが求めているのは A の支配的な固有ベクトルです。これは、任意の非退化開始ベクトルに A を繰り返し適用することで計算できます。
この簡略化されたランキング関数には、小さな問題があります。互いにリンクしているものの、他のページにはリンクしていない2つのウェブページを考えてみましょう。そして、そのうちの1つにリンクしているウェブページがあるとします。すると、反復処理中に、このループはランクを蓄積しますが、ランクを分配することはありません(アウトエッジがないため)。このループは、ランクシンクと呼ばれる一種の罠を形成します。
このランクシンクの問題を克服するために、ランクソースを導入します。
定義 1 \(E(u)\) を、ランクのソースに対応するウェブページ上のベクトルとする。 すると、ウェブページ集合の PageRank は、ウェブページへの割り当て \(R^\prime\) であり、次の式を満たす。 \[ R^\prime(u)=c\sum_{v\in B_u} \frac{R^\prime(v)}{N_v}+cR(u) \tag{1} \] \(c\) が最大化され、\(||R^\prime||_1 =1\)(\(||R^\prime||_1\) は \(R^\prime\) の \(L_1\) ノルムを表します)となる。
ここで、\(E(u)\) はウェブページ上のベクトルであり、ランクのソースに対応します(セクション 6 を参照)。\(E\) がすべて正の場合、方程式のバランスをとるために \(c\) を縮小する必要があることに注意してください。したがって、この手法は減衰係数に対応します。行列表記では、\(R^\prime = c(AR^\prime + E)\) となります。\(||R^\prime||_1 = 1\) であるため、これを \(R^\prime = c(A +E \times \mathbf{1})R^\prime\) と書き直すことができます。ここで、\(\mathbf{1}\) はすべて 1 からなるベクトルです。 したがって、\(R^\prime\) は \((A+ E \times \mathbf{1})\) の固有ベクトルです。
上記の PageRank の定義は、グラフ上のランダムウォークという直感的な根拠に基づいています。簡略化されたバージョンは、Web グラフ上のランダムウォークの定常確率分布に対応します。直感的には、これは「ランダムサーファー」の行動をモデル化したものと考えることができます。「ランダムサーファー」とは、単にランダムにリンクをクリックし続けるだけです。しかし、実際の Web サーファーが Web ページの小さなループに陥ったとしても、サーファーがそのループを永遠に続ける可能性は低いでしょう。代わりに、サーファーは他のページに移動します。追加の係数 \(E\) は、この行動をモデル化する方法として考えることができます。サーファーは定期的に「退屈」し、\(E\) の分布に基づいて選択されたランダムなページに移動します。
これまで、\(E\) はユーザー定義パラメータとして扱ってきました。ほとんどのテストでは、\(E\) はすべてのウェブページで均一で、値は \(\alpha\) とします。しかし、セクション6では、\(E\) の値を変えることで、どのように「カスタマイズされた」ページランクを生成できるかを示します。
スケールの問題を無視すれば、PageRankの計算は非常に簡単です。\(S\)をWebページ上のほぼ任意のベクトル(例えば\(E\))とします。PageRankは以下のように計算できます。 \[ \begin{align} R_0 &\leftarrow S \\ \\ loop: & \\ \\ R_{i+1} &\leftarrow AR_i \\ \\ d &\leftarrow ||R_i||_1 — ||R_{i+1}||_1 \\ \\ R_{i+1} &\leftarrow R_{i+1}+dE \\ \\ \delta &\leftarrow ||R_{i+1}-R_i||_1 \\ \\ while\; \delta \gt \epsilon & \end{align} \] \(d\) 係数は収束速度を高め、\(||R||_1\)を維持することに注意してください。別の正規化方法としては、\(R\) に適切な係数を乗じることです。\(d\) 係数の使用は、\(E\)の影響にわずかな影響を与える可能性があります。
このモデルの問題点の一つは、ダングリングリンクです。ダングリングリンクとは、外部リンクを持たない任意のページを指すリンクのことです。ダングリングリンクの重み付けが明確でなく、数が多いため、モデルに影響を与えます。多くの場合、これらのダングリングリンクは、Web全体をサンプリングすることが困難なため、まだダウンロードされていないページです(現在ダウンロードされている2,400万ページのうち、5,100万のURLがまだダウンロードされておらず、ダングリングリンクとなっています)。ダングリングリンクは他のページのランキングに直接影響を与えないため、すべてのPageRankが計算されるまで、システムから削除します。すべてのPageRankが計算された後、ダングリングリンクをシステムに戻しても、大きな影響はありません。削除されたリンクと同じページにある他のリンクの正規化はわずかに変化しますが、大きな影響はないでしょう。
スタンフォードWebBaseプロジェクト[PB98]の一環として、私たちは2400万ページのWebページをリポジトリに持つ完全なクロールおよびインデックス作成システムを構築しました。Webクローラーは、Web上のすべてのURLを発見できるようにURLのデータベースを保持する必要があります。PageRankを実装するには、Webクローラーがクロールしながらリンクのインデックスを作成するだけです。これは単純な作業ですが、膨大なデータ量を必要とするため、容易ではありません。例えば、現在2400万ページのデータベースを約5日間でインデックス化するには、1秒あたり約50ページのWebページを処理する必要があります。平均的なページには約11個のリンクがあるため(リンクの数え方によって異なります)、1秒あたり550個のリンクを処理する必要があります。また、2400万ページのデータベースは7500万を超える固有のURLを参照しており、各リンクはこれらのURLと比較する必要があります。
複雑かつ深刻な欠陥を抱えた多くのウェブ成果物に対して、システムの耐性を高めるために多くの時間を費やしてきました。膨大な数のサイト、ページ、そしてURLさえも存在します。多くのウェブページには誤ったHTMLが含まれており、パーサーの設計を困難にしています。クロールプロセスを支援するために、複雑なヒューリスティックが用いられています。例えば、/cgi-bin/を含むURLはクロールしません。もちろん、「ウェブ全体」は常に変化しているため、正確なサンプルを取得することは不可能です。サイトがダウンすることもあれば、インデックス登録を拒否する人もいます。こうした状況にもかかわらず、私たちは公開されているウェブの実際のリンク構造をある程度再現できていると考えています。
各 URL を一意の整数に変換し、各ハイパーリンクをデータベースに格納します。このデータベースでは、整数 ID を使用してページを識別します。実装の詳細は [PB98] に記載されています。一般的に、PageRank は次のように実装されています。まず、リンク構造を親 ID でソートします。次に、前述の理由により、リンク データベースから未結合リンクを削除します (数回の反復処理で、未結合リンクの大部分が削除されます)。ランクの初期割り当てを行う必要があります。この割り当ては、いくつかの戦略のいずれかで行うことができます。収束するまで反復処理を実行する場合、一般に初期値は最終値には影響せず、収束速度のみに影響します。しかし、適切な初期割り当てを選択することで収束を加速できます。初期割り当てを慎重に選択し、反復処理を少数の有限回数にすることで、優れたパフォーマンス、またはパフォーマンスの向上が得られると考えています。
各ページの重みにはメモリが割り当てられます。単精度浮動小数点値をそれぞれ4バイト使用するため、7,500万のURLでは300MBになります。すべての重みを保持するのに十分なRAMがない場合は、複数のパスを作成できます(この実装では、メモリを半分にし、2つのパスを使用します)。現在のタイムステップの重みはメモリに保持され、以前の重みにはディスク上で線形アクセスされます。また、リンクデータベースAへのアクセスはすべて線形です。これは、リンクデータベースAがソートされているためです。したがって、Aもディスク上に保持できます。これらのデータ構造は非常に大きいですが、線形ディスクアクセスにより、一般的なワークステーションでは各反復処理を約6分で完了できます。重みが収束した後、ダングリングリンクを戻してランキングを再計算します。ダングリングリンクを戻した後は、ダングリングリンクを削除するのに必要な回数だけ反復処理を実行する必要があることに注意してください。そうでなければ、一部のダングリングリンクの重みはゼロになります。現在の実装では、この処理全体に約5時間かかります。収束基準を緩和し、最適化を強化すれば、計算ははるかに高速化できます。あるいは、より効率的な固有ベクトル推定手法を用いることで、パフォーマンスを向上させることも可能です。ただし、PageRankの計算にかかるコストは、フルテキストインデックスの構築にかかるコストと比較するとごくわずかであることに留意する必要があります。
図4のグラフからわかるように、3億2,200万リンクの大規模データベースにおけるPageRankは、約52回の反復処理で妥当な許容範囲に収束します。データの半分の収束には約45回の反復処理が必要です。このグラフは、スケーリング係数が\(\log n\)にほぼ比例するため、PageRankは非常に大規模なコレクションであっても非常に良好にスケーリングできることを示唆しています。

PageRankの計算が急速に収束するという事実から生じる興味深い帰結の一つは、ウェブが拡張型グラフであるということです。これをより深く理解するために、グラフ上のランダムウォーク理論について簡単に概説します。詳細については、Motwani-Raghavan [MR95] を参照してください。グラフ上のランダムウォークとは、任意の時点においてグラフの特定のノードにいて、次の時点に訪れるノードを決定するために一様ランダムにアウトエッジを選択する確率過程です。ノードSのすべての(それほど大きくない)部分集合に、S内のノードから発するアウトエッジを介してアクセスできる頂点の集合である近傍が、ある係数a倍||よりも大きい場合、グラフは拡張型と呼ばれます。ここで、aは拡張係数と呼ばれます。グラフが良好な拡張係数を持つためには、最大の固有値が2番目に大きい固有値よりも十分に大きい必要があります。グラフ上のランダムウォークは、グラフ内のノード集合上の極限分布に急速に(グラフのサイズの対数的な時間で)収束する場合、急速混合型であると言われます。また、グラフがエクスパンダーであるか、固有値分離を持つ場合に限り、ランダムウォークがグラフ上で急速混合型となります。
これらすべてをPageRank計算に関連付けると、PageRank計算は本質的にWebグラフ上のランダムウォークの極限分布を決定するものであることに留意してください。ノードの重要度ランキングは、本質的に、ランダムウォークが十分に長い時間後にそのノードに到達する極限確率です。PageRank計算が対数時間で終了するという事実は、ランダムウォークが急速に混合している、あるいは基礎となるグラフが良好な拡張係数を持っていると言っているのと同じです。拡張グラフには、将来Webグラフを含む計算で利用できる可能性のある多くの望ましい特性があります。
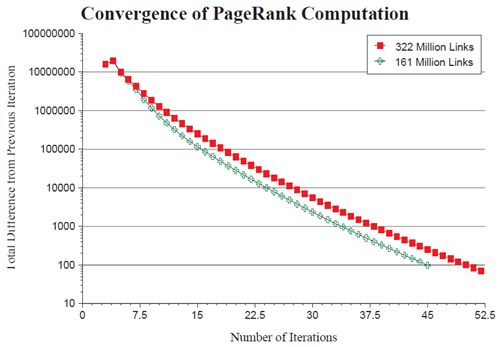
図5: フルサイズとハーフサイズのリンクデータベースの収束率
PageRankの主な用途は検索です。私たちはPageRankを使用する2つの検索エンジンを実装しました。1つ目は、シンプルなタイトルベースの検索エンジンです。2つ目は、Google [BP]と呼ばれる全文検索エンジンです。Googleは、標準的な検索インタラクション指標、近接性、アンカーテキスト(Webページへのリンクテキスト)、そしてPageRankなど、さまざまな要素を利用して検索結果をランク付けしています。PageRankの利点に関する包括的なユーザー調査は本稿の範囲を超えていますが、いくつかの比較実験を行い、その結果のサンプルを本稿で提供しています。
PageRank のメリットは、詳細が明確に指定されていないクエリで最も顕著になります。例えば、「スタンフォード大学」というクエリを実行すると、従来の検索エンジンではスタンフォード大学に言及しているウェブページ(出版物リストなど)がいくつも表示されますが、PageRank を使用すると、大学のホームページが最初に表示されます。
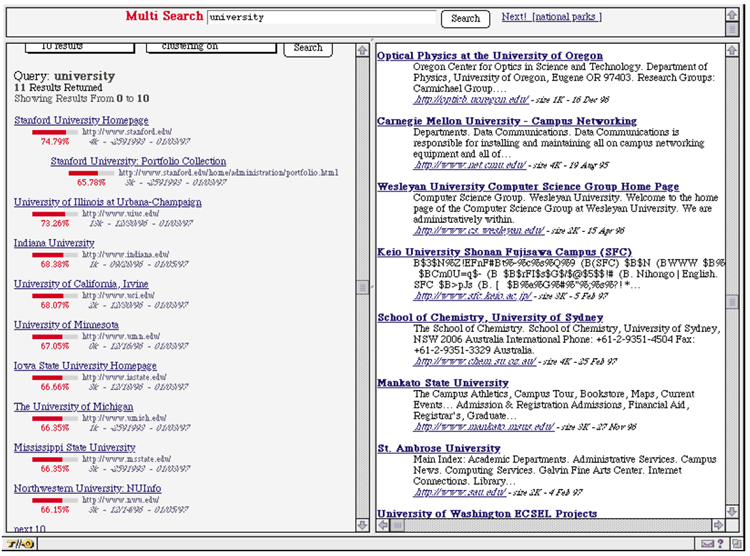
PageRankの検索における有用性をテストするため、1,600万のウェブページのタイトルのみを使用する検索エンジンを実装しました。クエリに答えるために、検索エンジンはタイトルにクエリ語をすべて含むすべてのウェブページを検索します。そして、結果をPageRankで並べ替えます。この検索エンジンは実装が非常に簡単で安価です。非公式なテストでは、非常にうまく機能しました。図6に示すように、「大学」を検索すると、上位の大学のリストが表示されます。この図は、ユーザーが2つの検索エンジンに同時にクエリを実行できるマルチクエリシステムを示しています。左側の検索エンジンは、PageRankベースのタイトル検索エンジンです。表示されている棒グラフとパーセンテージは、トップページを100%に正規化した実際のPageRankのログであり、本稿の他の部分で使用されているパーセンタイルではありません。右側の検索エンジンはAltavistaです。 Altavista が「大学」というクエリに一致し、サーバーのルートページであるランダムなウェブページを返していることがわかります(Altavista は URL の長さを品質ヒューリスティックとして使用しているようです)。
タイトルベースのPageRankシステムが非常にうまく機能する理由は、タイトルの一致によって高い精度が保証され、PageRankによって高品質が保証されるからです。Web上で「大学」のようなクエリを一致させる場合、ユーザーが確認できる範囲をはるかに超える情報が存在するため、再現率はそれほど重要ではありません。再現率がより重要となるより具体的な検索では、従来の情報検索が全文検索よりも重視され、PageRankを組み合わせる必要があります。Googleのシステムは、このようなランクの統合を行っています。ランクの統合は非常に難しい問題であることが知られており、この種のクエリを適切に評価できるようになるまでには、相当な追加作業が必要です。しかしながら、これらのクエリにおいてPageRankを要素として使用することは非常に有益であると考えています。
我々は、PageRank を使用する全文検索エンジンである Google を用いて、かなりの実験を行ってきました。 本格的なユーザー調査は本稿の範囲を超えていますが、付録 A にサンプルクエリを掲載しています。より多くのクエリについては、読者の皆様ご自身で Google をテストすることをお勧めします [BP]。
表1は、PageRankに基づく上位15ページを示しています。このリストは1996年7月に作成されました。最近のPageRankの計算では、MicrosoftがNetscapeをわずかに上回り、PageRankが最高位となりました。

PageRank の設計目標の一つは、クエリの一般的なケースを適切に処理することでした。例えば、ミシガン大学の学生がすべての管理機能に使用しているシステムが、wolverine(マーベル・コミックの架空のスーパーヒーロー)の名前を冠していることを思い出し、ユーザーが「wolverine」を検索したとします。PageRank ベースのタイトル検索システムは、最初の結果として「Wolverine Access」を返しました。これは理にかなっています。なぜなら、すべての学生が Wolverine Access システムを定期的に使用しており、ランダムなユーザーが「wolverine」というクエリで検索する可能性が非常に高いからです。Wolverine Access サイトが一般的なケースであるという事実は、ページの HTML には含まれていません。たとえページ内でこのような形式の適切なメタ情報を定義する方法があったとしても、ページ作成者がこの種の評価を信頼できないため、問題が生じます。多くの Web ページ作成者は、自分のページがすべて Web 上で最も優れ、最も使用されていると主張するだけでしょう。
wolverine に関する豊富な情報を含むサイトを見つけるという目標は、一般的な wolverine のサイトを見つけるという目標とは全く異なるタスクであることに注意することが重要です。Webのリンク構造を通じてテキストマッチングスコアを伝播させることで、あるトピックを詳細に議論しているサイトを見つけようとする興味深いシステムがあります(|[Mar97|)。このシステムは、最も中心的なパスにあるページを返そうとします。このシステムは、「花」のようなクエリに対して良好な結果をもたらします。システムは、花のトピックを詳細に扱っているサイトから、適切なナビゲーションページを返します。これを、花の買い方以外にほとんど情報のない、一般的に使用されている商用サイトを返すだけの一般的なアプローチと比較してください。私たちは、これらのタスクはどちらも重要であり、汎用Web検索エンジンは、これらのタスクの両方のニーズを自動的に満たす結果を返すべきだと考えています。本稿では、一般的なアプローチにのみ焦点を当てます。
PageRank がどのような一般的なケースシナリオを表現するのに役立つかを考えてみると、有益です。 Wolverine Access のような利用頻度の高いページ以外にも、PageRank は権威や信頼といった協調的な概念を表すことができます。例えば、ユーザーは、New York Times のホームページから直接リンクされているという理由だけで、あるニュース記事を好むかもしれません。もちろん、そのような記事は、非常に重要なページで言及されているという理由だけで、かなり高い PageRank を獲得するでしょう。これは、ある種の協調的な信頼を捉えているように思われます。なぜなら、ページが信頼できる、あるいは権威のある情報源によって言及されている場合、そのページは信頼できる、あるいは権威がある可能性が高いからです。同様に、品質や重要性も、このような循環的な定義に当てはまるようです。
PageRank計算の重要な要素は \(E\) です。\(E\) はWebページ上のベクトルで、アウトエッジのないサイクルなどのランクシンクを補うためのランクソースとして使用されます(セクション2.4を参照)。しかし、ランクシンクの問題を解決する以外にも、\(E\) はページランクを調整するための強力なパラメータであることがわかります。直感的に、\(E\) ベクトルは、ランダムなサーファーが定期的にジャンプするWebページの分布に対応します。以下に示すように、\(E\) ベクトルはWebの広範な概要を示すために、または特定の個人に焦点を当ててパーソナライズされたビューを提供するために使用できます。
ほとんどの実験は、すべてのウェブページで均一な \(E\) ベクトル(\(||E||_1 = 0.15\))を用いて行いました。これは、ランダムなサーファーが定期的にランダムなウェブページにジャンプする状況に相当します。 すべてのウェブページは存在するだけで評価されるため、\(E\) にとってこれは非常に民主的な選択です。 この手法は非常に成功していますが、重要な問題があります。関連リンクを多く含む一部のウェブページは、過度に高いランキング付けを受けます。このような例としては、著作権警告、免責事項、相互にリンクされたメーリングリストのアーカイブなどが挙げられます。
もう1つの極端な例は、\(E\)が完全に1つのWebページで構成されることです。私たちはそのような\(E\)を2つテストしました。Netscapeのホームページと、著名なコンピュータ科学者であるJohn McCarthyのホームページです。Netscapeのホームページについては、Netscapeをデフォルトのホームページに設定している初心者ユーザーの視点からページランクを生成しようとします。John McCarthyのホームページの場合は、ホームページ上のリンクに基づいてかなりのコンテキスト情報を提供してくれた個人の視点からページランクを計算したいと考えています。
どちらのケースでも、前述のメーリングリストの問題は発生しませんでした。また、どちらのケースでも、それぞれのホームページが最も高い PageRank を獲得し、その直下のリンクが続いていました。そこから格差は縮小しました。表 2 は、様々なページの PageRank パーセンタイルを示しています。コンピュータサイエンス関連のページは、Netscape ランクよりも McCarthy ランクが高く、スタンフォード大学のコンピュータサイエンス関連のページは McCarthy ランクがかなり高くなっています。例えば、スタンフォード大学のコンピュータサイエンス学科の他の教員の Web ページは、McCarthy ランクで 6 パーセンタイル以上高くなっています。ページランクはパーセンタイルで表示されていることに注意してください。これにより、範囲の上限における PageRank の大きな差が圧縮されます。

表2: 2つの異なる視点のページランク: Netscape vs. John McCarthy
このようなパーソナライズされたページランクは、パーソナル検索エンジンをはじめ、様々な用途に応用できます。これらの検索エンジンは、ブックマークやホームページといった簡単な入力から、ユーザーの興味関心の大部分を効率的に推測することで、ユーザーの手間を大幅に省くことができます。付録Aでは、「Mitchell」というクエリを用いて、この例を示しています。この例では、ウェブ上にはMitchellという名前の人が多数存在するにもかかわらず、検索結果の1位はJohn McCarthyの同僚であるJohn Mitchellのホームページであることを示しています。
このようなパーソナライズされたPageRankは、商業目的の操作を実質的に防ぎます。ページが高いPageRankを獲得するには、重要なページ、あるいは多くの重要でないページにリンクを張ってもらう必要があります。最悪の場合、重要なサイトで広告(リンク)を購入するという形で操作される可能性があります。しかし、費用がかかるため、これは十分に管理されているようです。 この操作に対する耐性は非常に重要な特性です。このような商業目的の操作は検索エンジンに大きな問題を引き起こし、あれば便利な機能の実装を非常に困難にしています。例えば、ドキュメントの高速更新は非常に望ましい機能ですが、検索エンジンの結果を操作しようとする人々によって悪用されています。
一様な \(E\) と単一ページ \(E\) という両極端の間の妥協案として、\(E\) をすべてのウェブサーバーのルートレベルページすべてで構成することが挙げられます。ただし、これにより PageRank をある程度操作できるようになることに注意してください。このシステムを操作したい人は、特定のサイトを指すルートレベルサーバーを多数作成するだけで済みます。
PageRankはランダムなウェブサーファーとほぼ一致するため(セクション2.5を参照)、PageRankが実際の利用状況とどのように一致するかを見ることは興味深いことです。NLANR [NLA]プロキシキャッシュからのウェブページアクセス数を使用し、PageRankと比較しました。NLANRデータは、数か月間にわたる複数の国内プロキシキャッシュから取得されたもので、11,817,665のユニークURLで構成されており、最もヒット数が多かったのはAltavistaで638,657ヒットでした。キャッシュデータと7,500万URLデータベースの共通部分には260万ページがありました。これらのデータセットを分析的に比較することは、いくつかの理由から非常に困難です。キャッシュアクセスデータ内のURLの多くは、無料メールサービスで個人メールを読んでいる人々です。サーバー名とページ名の重複は深刻な問題です。不完全性と偏りは、PageRankデータと利用状況データの両方に見られる問題です。しかし、データにはいくつか興味深い傾向が見られました。キャッシュデータではポルノサイトの利用率が高いようですが、これらのサイトのPageRankは概して低いです。これは、人々が自分のウェブページからポルノサイトにリンクしたくないためだと考えられます。PageRankと利用率の違いを探すこの手法を用いることで、人々が見たいと思っていても自分のウェブページでは触れたくないものを見つけることができるかもしれません。netscape.yahoo.comのように、利用率は非常に高いのにPageRankが低いサイトも存在します。おそらく、重要なバックリンクがデータベースから省略されているだけでしょう(ウェブのリンク構造は部分的なものしか持っていません)。利用率データをPageRankの開始ベクトルとして使用し、PageRankを数回反復処理することで、利用率データの欠落を埋めることができるかもしれません。いずれにせよ、このような比較は今後の研究にとって興味深いテーマです。
PageRank の正当性の一つは、被リンクの予測指標となることです。[|CGMP98] では、より質の高い文書をまずクロールすることで、ウェブを効率的にクロールする方法を探求しました。スタンフォード大学のウェブを対象としたテストでは、PageRank は引用数そのものよりも将来の引用数を予測する上で優れていることがわかりました。
この実験では、システムが単一のURLのみを持ち、その他の情報は何も持たない状態から開始し、可能な限り最適な順序でページをクロールすることを目標としています。 最適な順序とは、評価関数に基づいてランク付けされた順序でページをクロールすることです。ここでの目的のために、評価関数は完全な情報が与えられた場合の引用数です。ただし、評価関数を計算するために必要なすべての情報は、すべての文書がクロールされた後でなければ入手できないという難点があります。不完全なデータを用いた結果、PageRankは既知の引用数よりもクロール順序付けの順序付けに効果的な方法であることがわかりました。 言い換えれば、引用数を指標とする場合であっても、PageRankは引用数よりも優れた予測指標となるのです。この理由としては、PageRank が引用数のカウントが陥りやすい局所的な最大値を回避している点が挙げられます。例えば、引用数のカウントはスタンフォード大学のコンピュータサイエンスのウェブページのような局所的な集合体では行き詰まりがちで、他の領域で引用数の多いページを見つけるのに長い時間がかかります。PageRank はスタンフォード大学のホームページが重要であることを素早く認識し、その子ページを優先することで、効率的で広範な検索を実現します。
PageRankが引用数を予測する能力は、PageRankを使用する強力な根拠となります。Webの引用構造を完全にマッピングすることは非常に困難であるため、PageRankは引用数そのものよりも引用数の近似値として優れている可能性があります。
私たちは、ユーザーが目にする各リンクにPageRankを注釈として付与するWebプロキシアプリケーションを開発しました。これは非常に便利です。ユーザーはリンクをクリックする前に、そのリンクに関する情報を受け取ることができるからです。図7はプロキシのスクリーンショットです。赤いバーの長さはURLのPageRankの対数値です。スタンフォード大学のような主要な組織が非常に高いランキングを獲得しており、次に研究グループ、そして人物の順で、教授陣は人物スケールの上位に位置していることがわかります。また、ACMのPageRankは非常に高いものの、スタンフォード大学ほど高くないことにも注目してください。興味深いことに、このPageRank注釈付きページビューでは、教授の一人のURLが間違っていることが一目瞭然です。なぜなら、教授のPageRankは恥ずかしいほど低いからです。したがって、このツールはページの作成だけでなく、ナビゲーションにも役立つようです。このプロキシは、他の検索エンジンの結果や、Yahoo!のリストのようなリンクが多数あるページを確認するのに非常に役立ちます。プロキシは、長いリストの中からどのリンクが興味を引く可能性が高いかをユーザーが判断するのに役立ちます。また、ユーザーが探しているリンクが「重要度」のどのレベルに位置するかをある程度把握している場合は、プロキシを使用することで、より迅速にリンクをスキャンできるようになります。
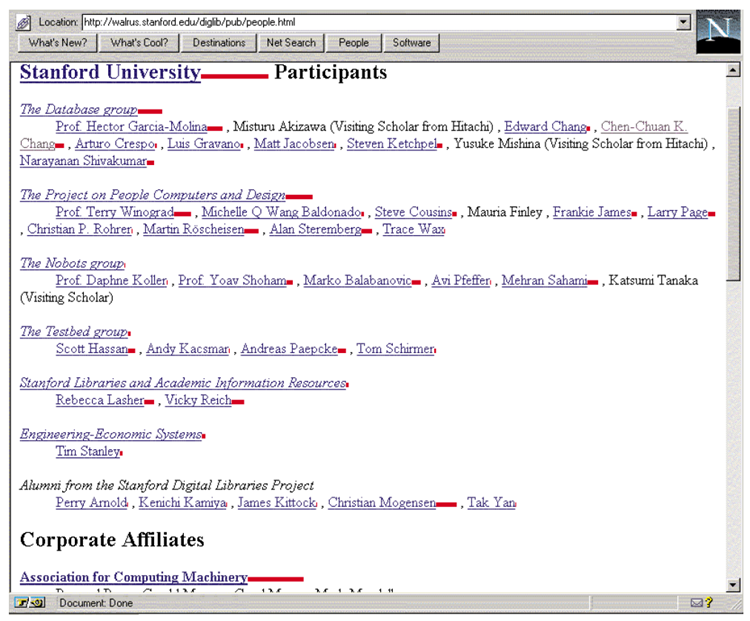
PageRankの本来の目的は、バックリンクを並べ替えることで、ある文書に多数のバックリンクがある場合に「最適な」バックリンクを最初に表示できるようにすることでした。私たちはそのようなシステムを実装しました。PageRankで順序付けられたバックリンクのこの表示は、競合他社を理解しようとするときに非常に興味深いものになることがわかりました。例えば、ニュースサイトを運営している人は、競合他社が獲得した重要なバックリンクを常に把握したいと考えています。また、PageRankは、ユーザーがサイトが信頼できるかどうかを判断するのに役立ちます。例えば、ユーザーはスタンフォード大学のホームページから直接引用された情報を信頼する傾向があるかもしれません。
本稿では、ワールド・ワイド・ウェブ上のあらゆるページを単一の数値、つまりPageRankに凝縮するという大胆な試みに挑戦しました。PageRankとは、ウェブのグラフ構造における位置のみに基づいて、コンテンツに関係なくすべてのウェブページをグローバルにランク付けするものです。
PageRank を用いることで、より重要で中心的なウェブページが優先されるように検索結果を順序付けることができます。実験では、これによりユーザーに高品質な検索結果が提供されることがわかりました。PageRank の背後にある直感的な考え方は、ウェブページ自体の外部にある情報、つまり一種のピアレビューとして機能するバックリンクを利用するというものです。さらに、「重要な」ページからのバックリンクは、平均的なページからのバックリンクよりも重要です。これは、PageRank の再帰的定義(セクション 2.4)に含まれています。
PageRank は、ほとんどのクエリに回答できる、一般的に使用される少数のドキュメントを分離するために使用できます。完全なデータベースを参照する必要があるのは、小規模なデータベースではクエリに回答できない場合にのみです。最後に、PageRank は、クラスターセンターに表示する代表的なページを見つけるのに役立つ可能性があります。
PageRankは、検索以外にも、トラフィック推定やユーザーナビゲーションなど、様々な用途に活用できることが分かっています。また、パーソナライズされたPageRankを生成することで、特定の視点からWebを分析することも可能です。
全体的に、PageRank に関する私たちの実験は、Web グラフの構造がさまざまな情報検索タスクに非常に有用であることを示唆しています。
この付録には、Google を用いたクエリ結果のサンプルがいくつか掲載されています。1 つ目は、統一された \(E\) を使用した「Digital Libraries」のクエリです。2 つ目は、John McCarthy のホームページのみを含む \(E\) を使用した「Mitchell」のクエリです。